주의점
- 왕복 거리를 구하는 것
- 모든 경우 따져야 하는 것
알고리즘 선택과 근거
- 플로이드 워셜
- 간선 최단 거리를 구해야하는 문제
- 모든 정점을 따져야한다.
- 다익스트라: 하나의 정점에서 모든 정점까지 최단거리
- 음수 불가
- 추후 탐색할 때 다익스트라 로직을 여러번 실행해야함
- 벨만포드: 하나의 정점에서 모든 정점까지 최단거리
- 음수 가능
- 음수 탐지 가능
- 문제는 두개의 정점(치킨집)을 구해야해서 여러번 계산해서 비효율적
- 플로이드: 여러개의 정점에서 여러개의 정점까지 최단거리
- 음수 가능
- But 음수 사이클은 불가
- 그러나 문제는 음수 사이클이 없음
- 음수 가능
- 다익스트라: 하나의 정점에서 모든 정점까지 최단거리
접근 방법 (플로이드 워셜)
플로이드 워셜 설명 (추후 링크로 변경)

문제 예시 1번으로 설명
Node (도시) 는 5개 Edge (도로) 는 4개 있다.
플로이드 워셜을 이용하기 위해 2차원 배열을 만들어준다.
자기 자신은 0으로 나머지는 임의의 큰 값으로 기입해준다. 사진에서는 편의상 MAX 로 표현한다.
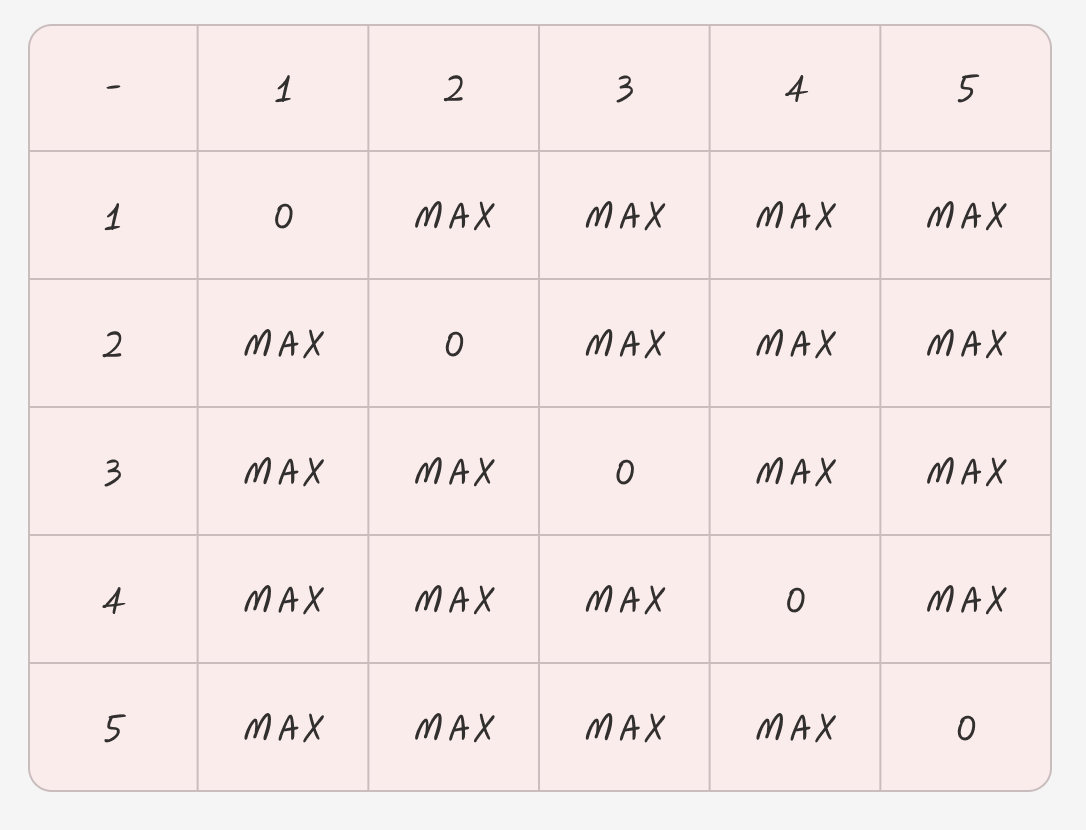
MAX 로 하는 이유는 최단 거리를 구해야하는 것이여서 비교할 때 정확한 값을 나오게 하기 위함이다.
이제 Edge 수 만큼 입력을 받아준다.
양방향 간선이므로 arr[A][B] 및 arr[B][A] 에도 1을 넣어준다.

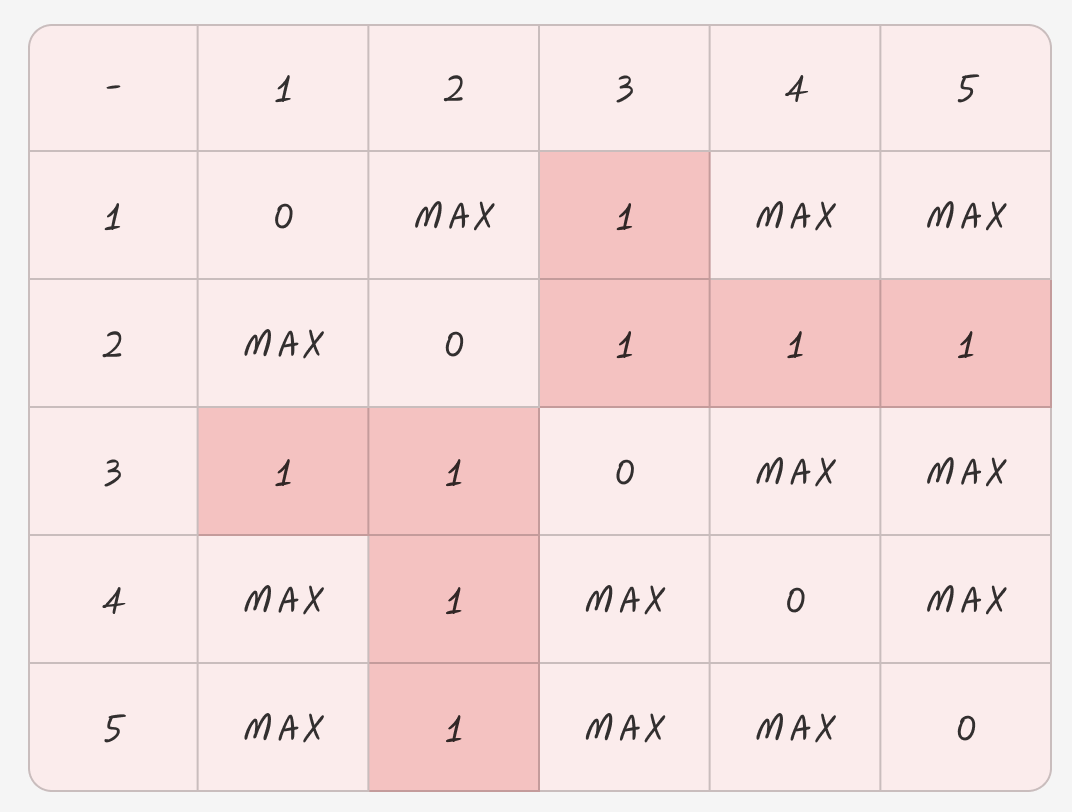
이렇게 초기화한 배열에 플로이드 워셜을 적용한다.
플로이드 워셜은 DP 라고 볼 수 있는데, 특정 조건을 위한 점화식이 있기 때문이다.
플로이드 워셜은 삼중 for문 으로 구현하며, 삼중 for문 예시는 다음과 같다.
for (int k = 1; k <= 노드수; k++) { // 기준 (더할 노드, 경유지라고 생각)
for (int a = 1; a <= 노드수; a++) { // 출발
for (int b = 1; b <= 노드수; b++) { // 도착
// a -> b 거리와 a -> k -> b 거리의 값을 비교
arr[a][b] = Math.min(arr[a][b], arr[a][k] + arr[k][b]);
}
}
}
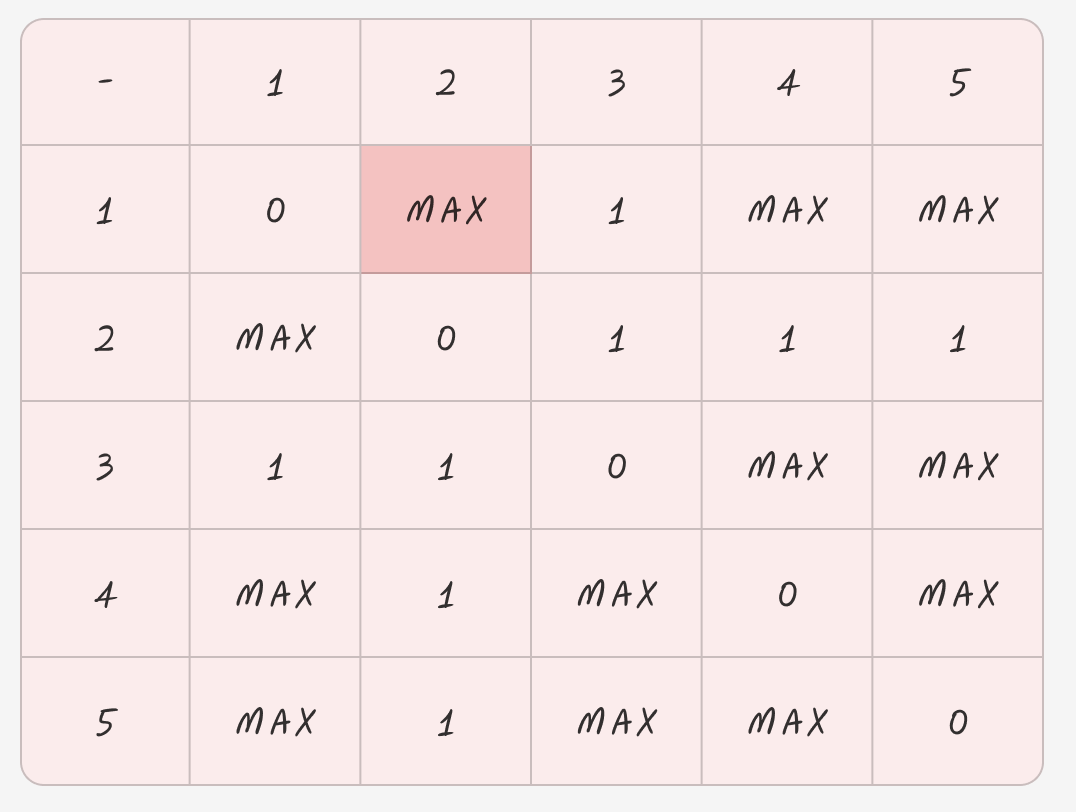
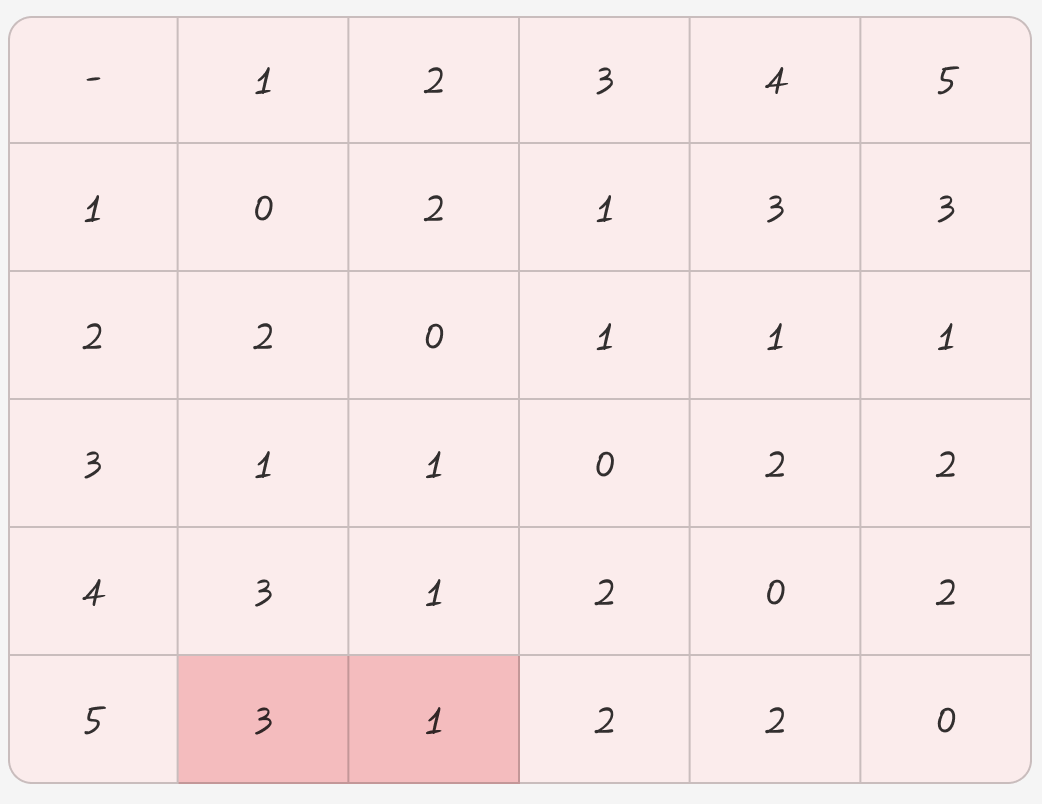
1 -> 2를 가는 최소 비용을 구할 것이다.
여기서 arr[1][2] 은 연결이 되지 않은 상태니, 연결된 것을 찾아야된다.
이건 모든 구간을 도니까 상관없다.
k = 3
a = 1
b = 2
라고 생각하자
그럼
1 -> 3 -> 2 인데
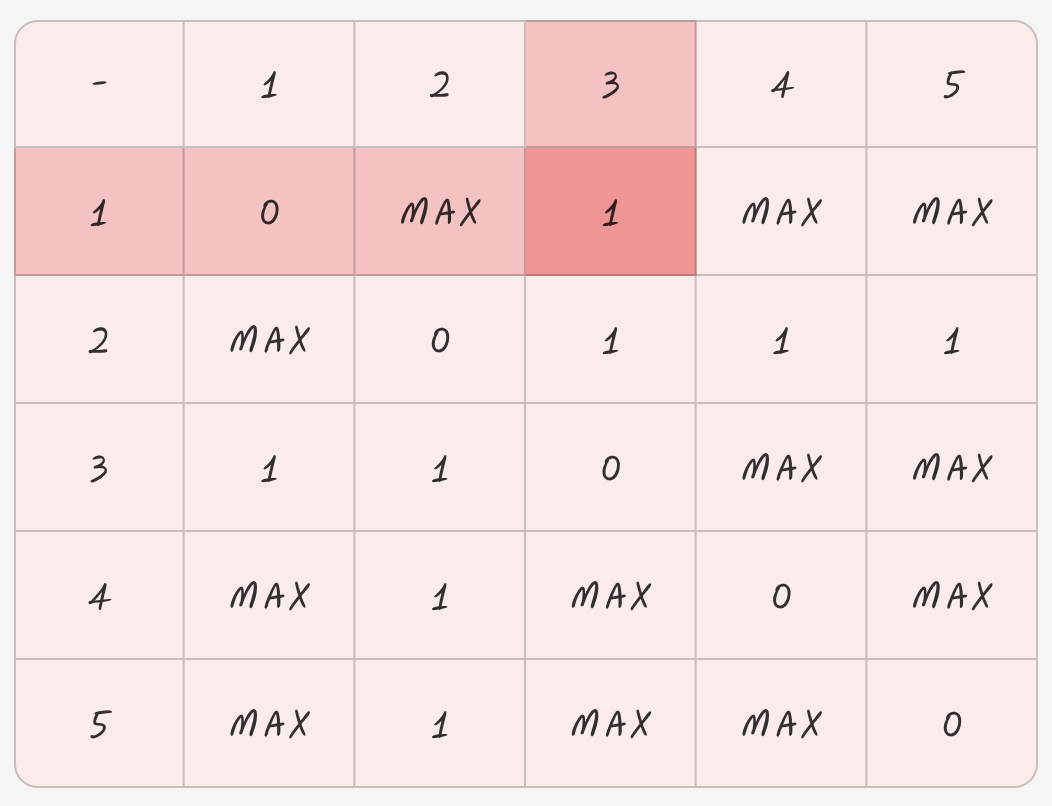
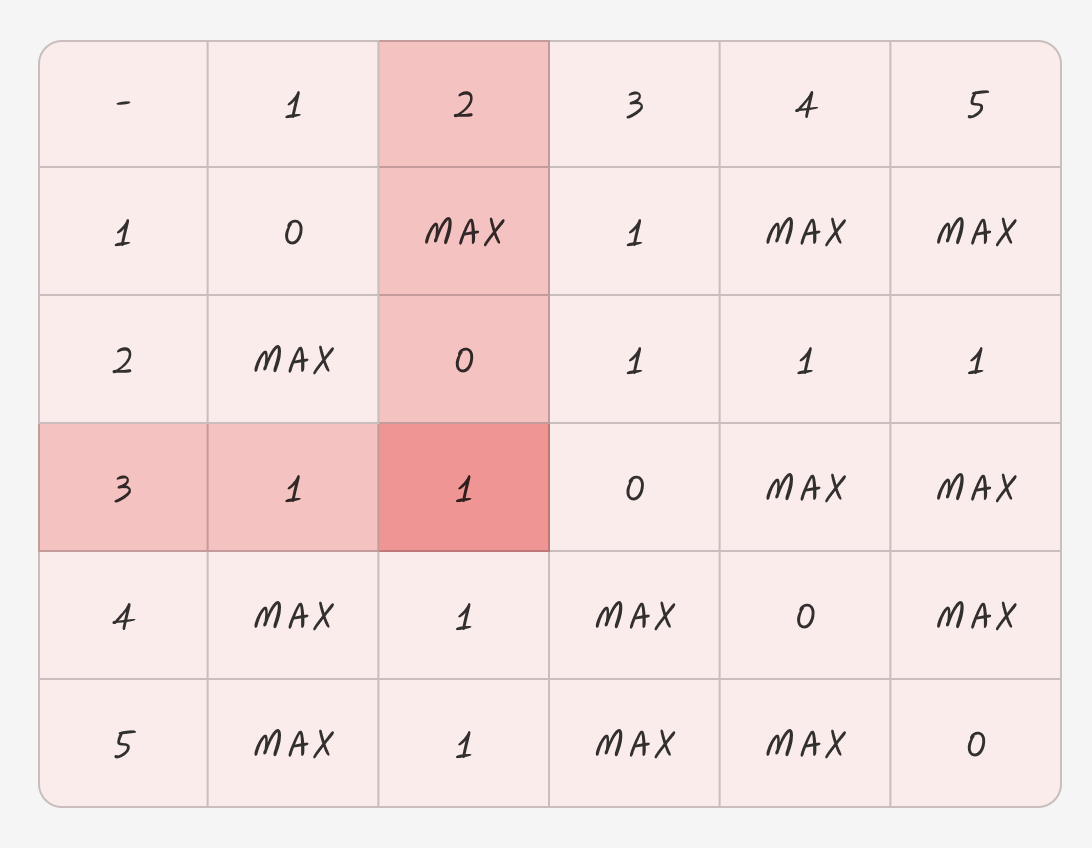
arr[1][2] = Math.min(MAX_VALUE, 1 + 1) 로 2가된다.
플로이드 워셜은 위 과정을 반복하여 각 경로별 최단 거리를 구한다.
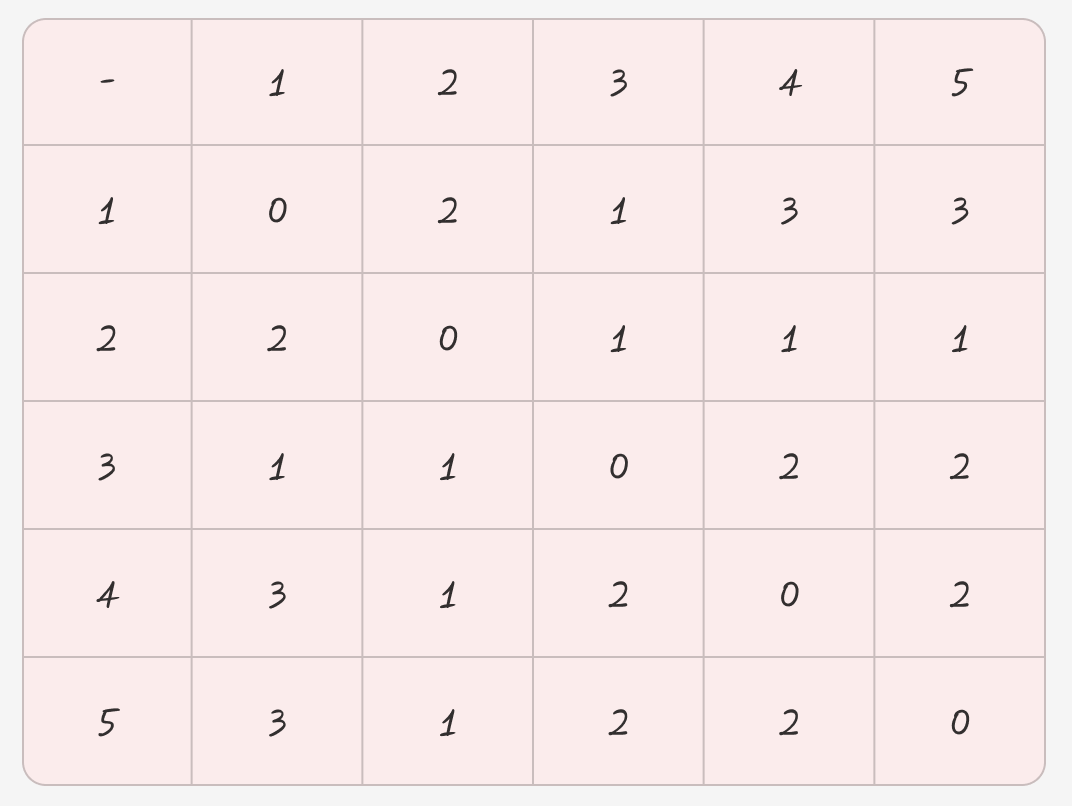
그럼 우리는 이렇게 얻은 플로이드 워셜을 가지고 치킨집을 어디에 배치할 것인지 구하면 된다.
우선, 3중 for문을 사용해야한다.
첫번째 for 문은 첫번째 치킨집 지정
두번째 for 문은 두번째 치킨집 지정
세번째 for 문은 각 지역별 가장 가까운 치킨집 거리다.
int sum = Integer.MAX_VALUE;
int[] result = new int[2];
// 치킨집 1
for (int i = 1; i <= N; i++) {
// 치킨집 2
for (int j = i + 1; j <= N; j++) {
int tmp = 0;
for (int k = 1; k <= N; k++) {
// 1(i)과 2(j)중에서 가장 짧은 치킨 집 선택
tmp += Math.min(arr[i][k], arr[j][k]);
}
// 가장 짧은 치킨집 우선 선택
// 가장 처음부터 for 문을 돌기 때문에 작은 숫자 먼저 나옴
if (sum > tmp) {
result[0] = i; // 1 번
result[1] = j; // 2 번
sum = tmp; // 최소 시간 (편도)
}
}
}
i = 1
j = 2
라고 가정하고 k를 돌아주면
1번과 2번은 둘 다 0이니 제외.
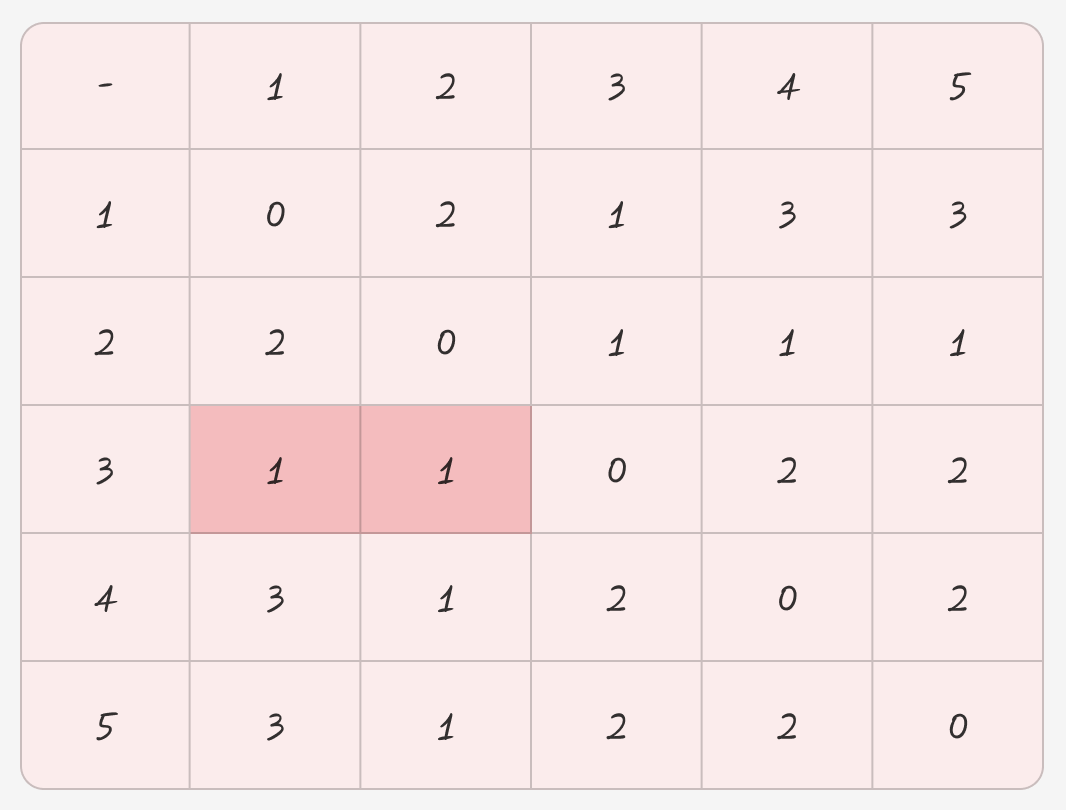
3에서 첫번째 치킨집 (1도시) 가는거랑 두번째 치킨집 (2도시) 가는 거리 중 가장 작은 값 선택
tmp += 1
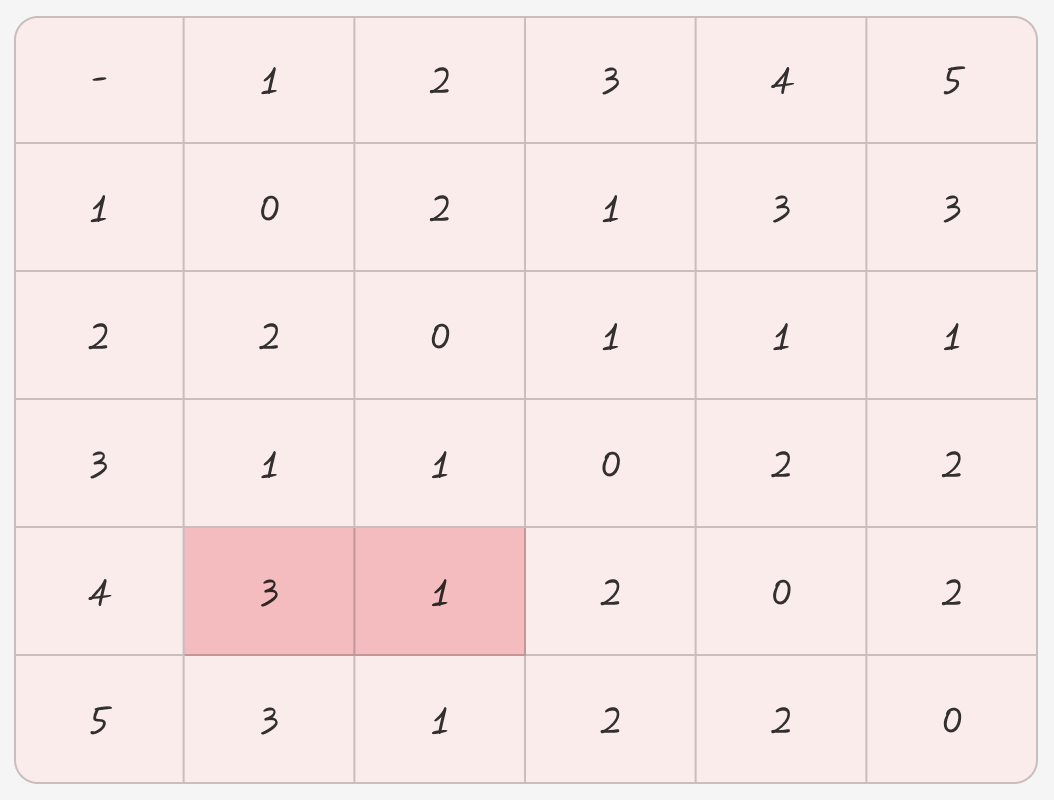
4에서 첫번째 치킨집 (1도시) 가는거랑 두번째 치킨집 (2도시) 가는 거리 중 가장 작은 값 선택
tmp += 1
5에서 첫번째 치킨집 (1도시) 가는거랑 두번째 치킨집 (2도시) 가는 거리 중 가장 작은 값 선택
tmp += 1
해서 총 3이 나온다.
tmp(=3) 값이 sum(MAX) 값 보다 적을 경우 sum 을 tmp 값으로 갱신
이 로직을 계속해서 반복해주면 된다.
정답 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class B_21278_호석이두마리치킨 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken()); // 도시
int M = Integer.parseInt(st.nextToken()); // 도로
// 플로이드 워셜 정리를 위한 2차원 배열
int[][] arr = new int[N + 1][N + 1];
for (int i = 0; i <= N; i++) {
Arrays.fill(arr[i], 10001);
arr[i][i] = 0;
}
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
arr[a][b] = 1;
arr[b][a] = 1;
}
// 플로이드 워셜 정리
for (int k = 1; k <= N; k++) {
for (int a = 1; a <= N; a++) {
for (int b = 1; b <= N; b++) {
arr[a][b] = Integer.min(arr[a][b], arr[a][k] + arr[b][k]);
}
}
}
int sum = Integer.MAX_VALUE;
int[] result = new int[2];
// 치킨집 1
for (int i = 1; i <= N; i++) {
// 치킨집 2
for (int j = i + 1; j <= N; j++) {
int tmp = 0;
for (int k = 1; k <= N; k++) {
// 1(i)과 2(j)중에서 가장 짧은 치킨 집 선택
tmp += Math.min(arr[i][k], arr[j][k]);
}
// 가장 짧은 치킨집 우선 선택
// 가장 처음부터 for 문을 돌기 때문에 작은 숫자 먼저 나옴
if (sum > tmp) {
result[0] = i; // 1 번
result[1] = j; // 2 번
sum = tmp; // 최소 시간 (편도)
}
}
}
System.out.println(result[0] + " " + result[1]);
System.out.println(sum * 2); // 편도 -> 왕복으로 출력
}
}'코딩테스트 > 백준' 카테고리의 다른 글
| [백준] 빌런 호석 (Java) (0) | 2024.12.30 |
|---|---|
| [백준] 퇴사 (Java) (0) | 2024.12.11 |
| [백준] 스타트와 링크 (Java) (0) | 2024.12.11 |
| [백준] 일곱 난쟁이 (Java) (0) | 2024.11.11 |
